JavaScript - binary search algorithm example

In this short article, we would like to show the main idea of the binary search algorithm providing example implementation in JavaScript.

1. Overview

Binary search is a fast search algorithm with run-time complexity O(log n). This algorithm requires working on sorted data with random access to each element.

2. Description

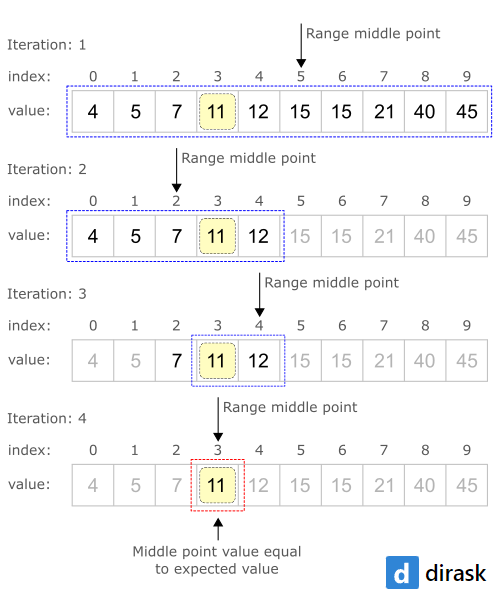
The main idea of the binary search algorithm is to:

1. find middle point index in actual range with the formula: 
   var point = Math.ceil((index + limit) / 2);
   Notes: 
   • actual range has been marked with a blue dashed border on the below image,
   • middle point index has been marked with a black arrow on the below image,
   • in the beginning, the actual range contains all array elements (index=0, limit=array.length-1),
   • the middle point index is used to split the searching problem into 2 smaller ranges - only if it is necessary for the next steps,
2. if the middle point value is equal to the expected value, the algorithm returns the middle point index,
   Notes:
   • expected value has been marked with a yellow rounded rectangle on the below image,
3. if the middle point value is not equal to the expected value, the range is split into left or right ranges with an excluded middle point, a new range that is likely to contain the expected value is selected as an actual range and we go back to 1. point (we work all-time on sorted data).
   Notes:
   • if the expected value is smaller than the middle point value we select left range,
   • if the expected value is bigger than the middle point value we select right range,

Algorithm iterations:

3. Custom iterative implementation example

// ONLINE-RUNNER:browser;

function searchIndex(array, value) {
	var index = 0;
  	var limit = array.length - 1;
  	while (index <= limit) {
        var point = Math.ceil((index + limit) / 2);
        var entry = array[point];
        if (value > entry) {
            index = point + 1;
            continue;
        }
        if (value < entry) {
            limit = point - 1;
            continue;
        }
        return point; // value == entry
    }
  	return -1;
}


// Usage example:

// for this implementation array must be sorted from smallest to biggest!
var array = [ 4, 5, 7, 11, 12, 15, 15, 21, 40, 45 ];
var index = searchIndex(array, 11); // we want to find index for 11

console.log(index);  // 3

4. Custom recursive implementation example

// ONLINE-RUNNER:browser;

function searchIndex(array, value) {
    function split(index, limit) {
        if (index > limit) {
            return -1;
        }
        var point = Math.ceil((limit + index) / 2);
        var entry = array[point];
        if (value < entry) {
            return split(index, point - 1);
        }
        if (value > entry) {
            return split(point + 1, limit);
        }
        return point; // value == entry
    }
  	return split(0, array.length - 1);
}


// Usage example:

// for this implementation array must be sorted from smallest to biggest!
var array = [ 4, 5, 7, 11, 12, 15, 15, 21, 40, 45 ];
var index = searchIndex(array, 11); // we want to find index for 11

console.log(index);  // 3